题目内容
6.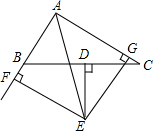 如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:
如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:(1)BF=CG;
(2)AB+AC=2AG.
分析 (1)连接EB、EC,利用已知条件证明Rt△BEF≌Rt△CEG,即可得到BF=CG;
(2)根据(1)中的条件证得Rt△AFE≌Rt△AGE,根据全等三角形的性质得到AG=AF,于是得到结论.
解答 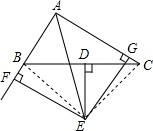 (1)证明:连接BE、EC,
(1)证明:连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB EG⊥AG,
且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
$\left\{\begin{array}{l}{BE=CE}\\{EF=EG}\end{array}\right.$,
∴Rt△BFE≌Rt△CGE (HL),
∴BF=CG;
(2)在Rt△AFE与Rt△AGE中,
$\left\{\begin{array}{l}{EF=EG}\\{AE=AE}\end{array}\right.$,
∴Rt△AFE≌Rt△AGE,
∴AG=AF,
∵AB+AC=AB+AG+CG=AB+AG+BF=AG+AF=2AG.
点评 本题考查了全等三角形的判定和性质,线段垂直平分线的性质,角平分线的性质,熟练正确全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
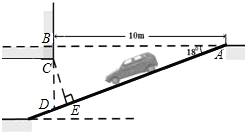 某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)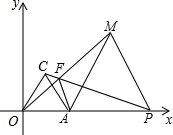 若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF.
若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F.求证:AF+MF=PF.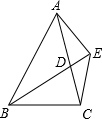 如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )
如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.则下列结论正确的是:①△ABD≌△EBC;②S△ABD=S△BDC;③∠BCE+∠BCD=180°;④AD=AE=EC;其中正确的是( )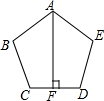 如图,正五边形ABCDE中,AF⊥CD,垂足为F
如图,正五边形ABCDE中,AF⊥CD,垂足为F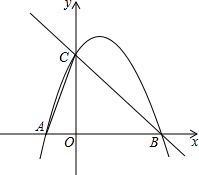 如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,己知抛物线与x轴分别交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).