题目内容
13.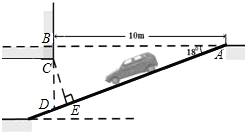 某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)
某居民小区为缓解居民停车难问题为缓解“停车难”问题,拟造地下停车库,如图是地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5.根据规定,地下停车库破道口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.请根据以上数据,求出该地下停车库限高CE的长.(结果精确到0.1米)(sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
分析 由三角函数求出BD,得出CD的长,由直角三角形的性质求出∠DCE=18°,由三角函数求出CE的长即可.
解答 解:∵AB⊥BD,
∴∠ABD=90°,
∴BD=AB•tan∠BAD=10×tan18°=3.2(m),
∴CD=BD-BC=3.2-0.5=2.7(m),
∵∠BAD+∠BDA=∠DCE+∠BDA=90°,
∴∠DCE=18°,
∴CE=CD•cos∠DCE=2.7×cos18°=2.7×0.95≈2.6(m),
即该地下停车库限高CE的长约为2.6m.
点评 此题考查了解直角三角形的应用,熟练掌握三角函数在解直角三角形中的应用是解答本题的关键,难度一般.

练习册系列答案
相关题目
 把图分成大小、形状完全相同的两块,且使每块中都含“奋发图强”这4个字,请你试一试,画出分界线.
把图分成大小、形状完全相同的两块,且使每块中都含“奋发图强”这4个字,请你试一试,画出分界线. 如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM.
如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM.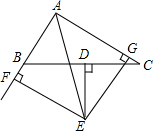 如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证:
如图,已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB的延长线于点F,EG⊥AC于点G,求证: