题目内容
6.菱形的一个内角为60°,它的边长是2cm,则这个菱形的面积是2$\sqrt{3}$cm2.分析 先求菱形的高,再运用公式:底×高计算.可画出草图分析.
解答 解:如图,∠B=60°,AB=BC=2cm,
作AE⊥BC于E,则AE=AB•sinB=2×sin60°=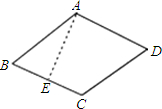 $\sqrt{3}$,
$\sqrt{3}$,
∴面积S=BC•AE=2×$\sqrt{3}$=2$\sqrt{3}$(cm2),
故答案为:2$\sqrt{3}$.
点评 本题考查的是菱形的面积求法.菱形的面积有两种求法:(1)利用底乘以相应底上的高;(2)利用菱形的特殊性,菱形面积=$\frac{1}{2}$×两条对角线的乘积.具体用哪种方法要看已知条件来选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在平面直角坐标系中,直线y=kx+1(k≠0)一定不同时经过( )
| A. | 第一、第二象限 | B. | 第二、第三象限 | C. | 第三、第四象限 | D. | 第一、第四象限 |
11.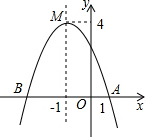 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
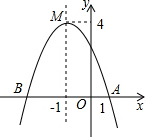 如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )
如图,函数y=ax2+bx+c(a≠0)的图象与x轴相交于A、B两点,頂点为点M.則下列说法不正确的是( )| A. | a<0 | B. | 当x=-1时,函数y有最小值4 | ||
| C. | 对称轴是直线=-1 | D. | 点B的坐标为(-3,0) |
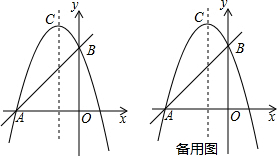
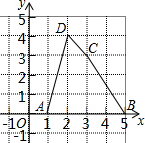 在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4).
在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4).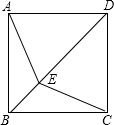 如图,在正方形ABCD中,点E是对角线BD上的点,求证:△ABE≌△CBE.
如图,在正方形ABCD中,点E是对角线BD上的点,求证:△ABE≌△CBE.