题目内容
15．
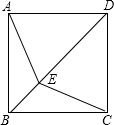如图，在正方形ABCD中，点E是对角线BD上的点，求证：△ABE≌△CBE．
分析 利用正方形的性质和SAS证明△ABE≌△CBE即可．
解答 证明：正方形ABCD中，AB=CB，∠ABE=∠CBE，
又∵BE=BE，
在△ABE和△CBE中，
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBE}\\{BE=BE}\end{array}\right.$，
∴△ABE≌△CBE（SAS）．
点评 本题利用了全等三角形的判定，关键是根据正方形的性质和SAS证明．
练习册系列答案
相关题目
5．$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$是下列哪个方程组的解（ ）
| A． | $\left\{\begin{array}{l}{2x-y=1}\\{3x+4y=4}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{2x+y=10}\\{3x+4y=20}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{2x-y=1}\\{3x-4y=4}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2x+y=0}\\{3x-4y=-4}\end{array}\right.$ |
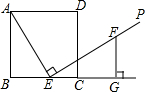如图，E是正方形ABCD的边BC上的一个动点（E与B、C两点不重合），过点E作射线EP⊥AE，在射线EP上截取线段EF，使得EF=AE，过点F作FG⊥BC交BC的延长线于点G．
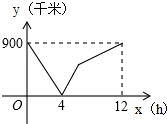一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，两车的距离y（千米）与慢车行驶的时间为x（小时）之间的函数关系如图所示，则快车到达乙地时慢车离乙地距离为450千米．
7．菱形和矩形一定具备的性质是（ ）
| A． | 对角线互相平分 | B． | 对角线互相垂直 | ||
| C． | 对角线相等 | D． | 每条对角线平分一组对角 |
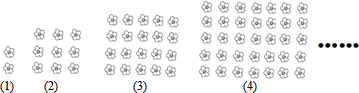
摆成的一组有规律的图案，按图中规律，第n个图形中小梅花的个数是（2n-1）（n+1）．