题目内容
1.如图,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3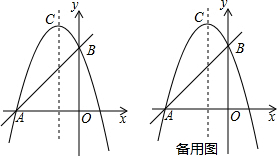
(1)求抛物线的函数表达式及其顶点C的坐标;
(2)如图,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形以AB为腰的等腰三角形?若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
分析 (1)先根据直线y=x+3求出A、B两点的坐标,然后将它们代入抛物线中即可求出待定系数的值,根据抛物线的解析式可求出C的坐标;
(2)分别从AB=BQ,AQ=BQ,AB=AQ三方面去分析,注意抓住线段的求解方法,借助于方程求解即可求得答案.
解答 解:(1)由经过点A,B的直线的表达式为y=x+3.可知A(-3,0),B(0,3),
∵抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,
∴$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$,
解得:b=-2,c=3,
∴抛物线的解析式为:y=-x2-2x+3,
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C(-1,4);
(2)存在;
理由:∵A(-3,0),B(0,3),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵Q在直线x=-1上,
∴设Q(-1,n),
∵点A,B,Q构成的三角形是以AB为腰的等腰三角形,
①当AQ=AB=3$\sqrt{2}$,
∴22+n2=(3$\sqrt{2}$)2,
∴n=$\sqrt{14}$,或n=-$\sqrt{14}$,
②当BQ=AB=3$\sqrt{2}$,
∴12+(3-n)2=(3$\sqrt{2}$)2
∴n=3+$\sqrt{17}$,或n=3-$\sqrt{17}$,
∴Q(-1,$\sqrt{14}$);(-1,-$\sqrt{14}$);(-1,3+$\sqrt{17}$)或(-1,3-$\sqrt{17}$).
点评 此题考查了待定系数法求二次函数的解析式与等腰三角形的性质等知识.此题难度适中,注意分类讨论思想,方程思想与数形结合思想的应用是解此题的关键,还要注意别漏.

 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
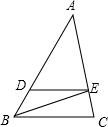 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母常年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母常年在外打工,孩子带在身边 | 20 | 10% |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |
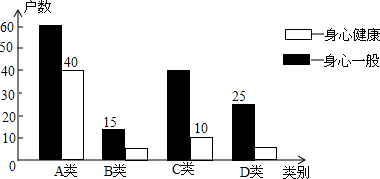
请你用学过的统计知识,解决问题:
(1)记者走访了边远山区多少家农户?
(2)将统计表中的空缺数据填写完整;
(3)分析数据后,你能得出什么结论?
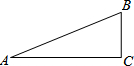 如图,在一坡比为1:3的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为$\sqrt{10}$米.
如图,在一坡比为1:3的斜坡上种有两棵小树,它们之间的距离AB为10米,则这两棵树的高度差BC为$\sqrt{10}$米.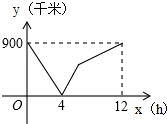 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.