题目内容
17.在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②-①得2S-S=27-1,S=27-1,即1+2+22+23+24+25+26=27-1.(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
分析 (1)将1+3+32+33+34+35+36乘3,减去1+3+32+33+34+35+36,把它们的结果除以3-1=2即可求解;
(2)将1+a+a2+a3+…+a2013乘a,减去1+a+a2+a3+…+a2013,把它们的结果除以a-1即可求解.
解答 解:(1)1+3+32+33+34+35+36
=[(1+3+32+33+34+35+36)×3-(1+3+32+33+34+35+36)]÷(3-1)
=[(3+32+33+34+35+36+37)-(1+3+32+33+34+35+36)]÷2
=(37-1)÷2
=2186÷2
=1093;
(2)1+a+a2+a3+…+a2013(a≠0且a≠1)
═[(1+a+a2+a3+…+a2013)×a-(1+a+a2+a3+…+a2013)]÷(a-1)
=[(a+a2+a3+…+a2013+a2014)-(1+a+a2+a3+…+a2013)]÷(a-1)
=(a2014-1)÷(a-1)
=$\frac{{a}^{2014}-1}{a-1}$.
点评 本题考查了整式的混合运算,有理数的乘方,读懂题目信息,理解等比数列的求和方法是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
8.随着网络时代的到来,很多家庭都接入了网络,电信局规定了拨号入网两种收费方式,用户可以任选其一:
①某用户某月上网的时间为x分钟,A、B两种收费方式的费用分别为y1(元)、y2(元),写出y1、y2与x之间的函数关系式.
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
①某用户某月上网的时间为x分钟,A、B两种收费方式的费用分别为y1(元)、y2(元),写出y1、y2与x之间的函数关系式.
②在上网时间相同的条件下,请你帮该用户选择哪种方式上网更省钱?
| 月租费(元) | 计费方式(元/分) | |
| A方式 | 0 | 0.05 |
| B方式 | 54 | 0.02 |
5.$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$是下列哪个方程组的解( )
| A. | $\left\{\begin{array}{l}{2x-y=1}\\{3x+4y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=10}\\{3x+4y=20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{2x-y=1}\\{3x-4y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=0}\\{3x-4y=-4}\end{array}\right.$ |
12. 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
 矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )
矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC=8,则△ABO的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
9.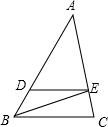 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
 如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )
如图,在△ABC中,DE∥BC,∠DBE=30°,∠EBC=25°,则∠ADE为( )| A. | 65° | B. | 55° | C. | 45° | D. | 75° |
7.菱形和矩形一定具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 每条对角线平分一组对角 |