题目内容
16.p为什么数时,关于x的方程7x2-(p+13)x+p2-p-2=0的两根α、β分别满足0<α<1,1<β<2.分析 设f(x)=7x2-(m+13)x+m2-m-2,则由题意可分三种情况:f(0)>0,f(1)<0,f(2)>0,解不等式求得实数p的取值范围即可.
解答 解:设f(x)=7x2-(p+13)x+p2-p-2,则f(x)=0的两根α、β分别满足0<α<1,1<β<2.
需要:f(0)>0,
则p2-p-2>0,
解得p>2或p<-1;
f(1)<0,
则7-(p+13)+p2-p-2<0,
解得-2<p<4;
f(2)>0,
则28-2(p+13)+p2-p-2>0,
解得p>3或p<0.
综上可知:则p的范围是:-2<p<-1或3<p<4.
点评 本题主要考查了抛物线和x轴交点的问题,用到的知识点有一元二次方程根的分布与系数的关系,体现了转化和分类的数学思想,属于中档题,解题的关键是掌握函数与x轴的交点的横坐标就是方程的根,两者互相转化,要充分运用这一点来解题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
7.菱形和矩形一定具备的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 每条对角线平分一组对角 |
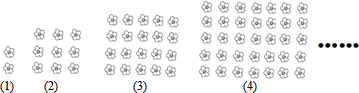
 摆成的一组有规律的图案,按图中规律,第n个图形中小梅花的个数是(2n-1)(n+1).
摆成的一组有规律的图案,按图中规律,第n个图形中小梅花的个数是(2n-1)(n+1).