题目内容
1.已知a,b,c均为有理数,若a>b,且b≠0,则下列结论不一定成立的是( )| A. | a2>ab | B. | a+c>b+c | C. | $\frac{a}{c^2}>\frac{b}{c^2}$ | D. | c-a<c-b |
分析 根据不等式的性质3,可判断A;根据不等式的性质1,可判断B;根据不等式的性质2,可判断C;根据不等式的性质1,性质3,可判断D.
解答 解:A、若a>b,a小于0时,不成立,故A不正确;
B、由不等式的性质1,若a>b,a+c<b+c,故B正确;
C、由不等式的性质2,若a>b,$\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$故C正确;
D、由不等式的性质3,若a>b,-a<-b,由不等式的性质1,c-a<c-b故D正确;
故选A.
点评 本题考查了不等式的性质,注意不等式的两边都成一或除以同一个负数,不等号的方向改变是解答此题的关键.

练习册系列答案
相关题目
9.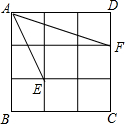 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )| A. | 30° | B. | 45° | C. | 60° | D. | 35° |
 某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?
某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?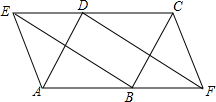 如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF
如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF 如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.
如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.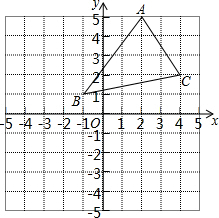 如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.
如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.



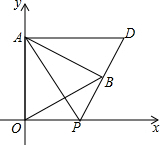 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.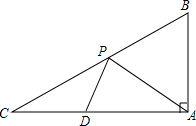 如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.
如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.