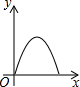题目内容
9.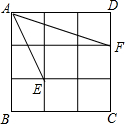 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )| A. | 30° | B. | 45° | C. | 60° | D. | 35° |
分析 连结EF,分别在格点三角形中,根据勾股定理即可得到AE,EF,AF的长度,继而可得出∠EAF的度数.
解答  解:连结EF.
解:连结EF.
根据勾股定理可以得到:AE=EF=$\sqrt{5}$,AF=$\sqrt{10}$.
∵($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,
∴AE2+EF2=AF2,
∴△AEF是等腰直角三角形.
∴∠EAF=45°.
故选:B.
点评 本题考查了勾股定理及其逆定理,判断△AEF是等腰直角三角形是解决本题的关键.

练习册系列答案
相关题目
19.一次函数y=-2x-3的图象经过的象限是( )
| A. | 一、二、三 | B. | 一、二、四 | C. | 一、三、四 | D. | 二、三、四 |
17. 如图,AD∥BC∥x轴,下列说法正确的是( )
如图,AD∥BC∥x轴,下列说法正确的是( )
 如图,AD∥BC∥x轴,下列说法正确的是( )
如图,AD∥BC∥x轴,下列说法正确的是( )| A. | A与D的横坐标相同 | B. | C与D的横坐标相同 | ||
| C. | B与C的纵坐标相同 | D. | B与D的纵坐标相同 |
4.为了帮助农村贫困家庭子女完成初中学业,国家给他们免费提供教科书,下表是某中学免费提供教科书补助的部分情况:
求获得免费提供教科书补助的七年级和八年级的人数.
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | - |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
1.已知a,b,c均为有理数,若a>b,且b≠0,则下列结论不一定成立的是( )
| A. | a2>ab | B. | a+c>b+c | C. | $\frac{a}{c^2}>\frac{b}{c^2}$ | D. | c-a<c-b |
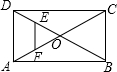 如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm.
如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm. cm.
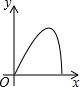
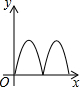
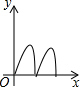
cm.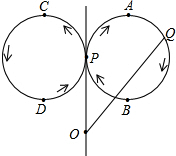 如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )