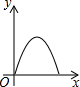题目内容
2.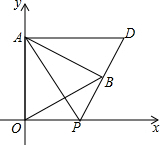 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.求:DP的长及点D的坐标.
分析 根据等边三角形的每一个角都是60°可得∠OAB=60°,然后根据对应边的夹角∠OAB为旋转角求出∠PAD=60°,再判断出△APD是等边三角形,根据等边三角形的三条边都相等可得DP=AP,根据,∠OAB的平分线交x轴于点P,∠OAP=30°,利用三角函数求出AP,从而得到DP,再求出∠OAD=90°,然后写出点D的坐标即可.
解答 解:∵△AOB是等边三角形,
∴∠OAB=60°,
∵△AOP绕着点A按逆时针方向旋转边AO与AB重合,
∴旋转角=∠OAB=∠PAD=60°,AD=AP,
∴△APD是等边三角形,
∴DP=AP,∠PAD=60°,
∵A的坐标是(0,3),∠OAB的平分线交x轴于点P,
∴∠OAP=30°,AP=$\sqrt{{(\sqrt{3})}^{2}+{3}^{2}}$=2$\sqrt{3}$,
∴DP=AP=2$\sqrt{3}$,
∵∠OAP=30°,∠PAD=60°,
∴∠OAD=30°+60°=90°,
∴点D的坐标为(2$\sqrt{3}$,3).
点评 本题考查了旋转的性质,坐标与图形性质,等边三角形的判定与性质,解直角三角形,熟记各性质并判断出△APD是等边三角形是解题的关键.

练习册系列答案
相关题目
1.已知a,b,c均为有理数,若a>b,且b≠0,则下列结论不一定成立的是( )
| A. | a2>ab | B. | a+c>b+c | C. | $\frac{a}{c^2}>\frac{b}{c^2}$ | D. | c-a<c-b |
7.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (x+y)2=x2+y2 | C. | (a3b)2=a6b2 | D. | a2÷a3=a(a≠0) |
12.已知$\frac{1}{a}$-$\frac{1}{b}$=4,则$\frac{a-2ab-b}{2a+7ab-2b}$的值等于( )
| A. | 6 | B. | -6 | C. | $\frac{2}{15}$ | D. | -$\frac{2}{7}$ |
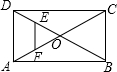 如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm.
如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm.
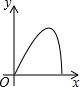
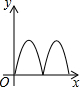
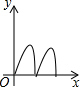
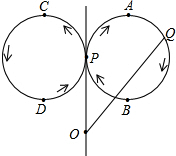 如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )