题目内容
12.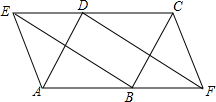 如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF
如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF(1)求证:四边形DEBF为平行四边形;
(2)当以平行四边形ABCD的边分别向外作以AD、BC为底的等腰三角形时,上述结论是否仍然成立,为什么?
(3)结合(1)(2)提出一个新的问题使四边形DEBF为平行四边形.
分析 (1)根据平行四边形的判定方法:两组对边相等的四边形是平行四边形即可证明四边形DEBF是平行四边形;
(2)利用(1)中所求,结合无法得出△EAB≌△DCF,故无法得出BE=FD,进而得出结论;
(3)利用(1)中所求,结合等腰直角三角形的性质求出即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,∠DAB=∠DCB,
∵以AD、BC为边分别向外作等边△ADE和等边△BCF,
∴AD=DE=AE,BF=BC=FC,
∴AE=CF,
∵∠EAB=∠DAB+∠DAE,∠DCF=∠DCB+∠BCF,
∴∠EAB=∠DCF,
在△EAB和△DCF中,
∵$\left\{\begin{array}{l}{AE=CF}\\{∠EAB=∠DCF}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△DCF(SAS),
∴BE=FD,
∴四边形DEBF是平行四边形;
(2)解:当以平行四边形ABCD的边分别向外作以AD、BC为底的等腰三角形时,上述结论不成立,
∵等腰三角形的腰长不确定,则无法得出△EAB≌△DCF,故无法得出BE=FD,则无法得出四边形DEBF是平行四边形;
(3)解:当以平行四边形ABCD的边分别向外作以AD、BC为斜边的等腰直角三角形时,四边形DEBF为平行四边形.
理由:∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,∠DAB=∠DCB,
∵以AD、BC为斜边分别向外作等腰直角三角形ADE和等腰直角三角形BCF,
∴DE=AE=$\frac{\sqrt{2}}{2}$AD,BF=FC=$\frac{\sqrt{2}}{2}$BC,
∴AE=CF,
∵∠EAB=∠DAB+∠DAE,∠DCF=∠DCB+∠BCF,
∴∠EAB=∠DCF,
在△EAB和△DCF中,
∵$\left\{\begin{array}{l}{AE=CF}\\{∠EAB=∠DCF}\\{AB=DC}\end{array}\right.$,
∴△EAB≌△DCF(SAS),
∴BE=FD,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边形的判定和性质、全等三角形的判定和性质,解题的关键是熟记平行四边形的判定方法,并且灵活运用判定方法.

 如图,AD∥BC∥x轴,下列说法正确的是( )
如图,AD∥BC∥x轴,下列说法正确的是( )| A. | A与D的横坐标相同 | B. | C与D的横坐标相同 | ||
| C. | B与C的纵坐标相同 | D. | B与D的纵坐标相同 |
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | - |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
| A. | a2>ab | B. | a+c>b+c | C. | $\frac{a}{c^2}>\frac{b}{c^2}$ | D. | c-a<c-b |
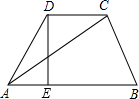 如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.
如图,在梯形ABCD中,DC∥AB,DE⊥AB,DC=2,AC=$\sqrt{19}$,∠DAE=60°,则DE=$\frac{3\sqrt{3}}{2}$.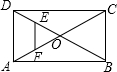 如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm.
如图,在矩形ABCD中,对角线AC和BD相交于点O,点E、F分别是DO、AO的中点.若AB=8cm,BC=4cm,则△OEF的周长为(2$\sqrt{5}$+2)cm. 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.