题目内容
6.如图将4个长、宽分别为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )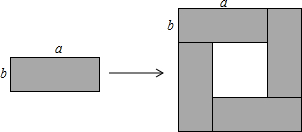
| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | 4ab=(a+b)2-(a-b)2 |
分析 根据图形的组成以及正方形和长方形的面积公式,知:大正方形的面积-小正方形的面积=4个矩形的面积.
解答 解:∵大正方形的面积-小正方形的面积=4个矩形的面积,
∴(a+b)2-(a-b)2=4ab,即4ab=(a+b)2-(a-b)2.
故选D.
点评 此题考查了完全平方公式的几何背景,能够正确找到大正方形和小正方形的边长是难点.解决问题的关键是读懂题意,找到所求的量的等量关系.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1. 如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
 如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
11.当△ABC和△DEF具备( )条件时,△ABC≌△DEF.
| A. | 所有的角对应相等 | B. | 三条边对应相等 | ||
| C. | 面积相等 | D. | 周长相等 |
18.正数5的算术平方根是( )
| A. | ±$\sqrt{5}$ | B. | ±$\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
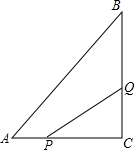 如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.