题目内容
1. 如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 由DE∥BC,推出△ADE∽△ABC,推出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AE}{AC}$)2,由S△ADE:S四边形DBCE=1:8,推出S△ADE:S△ABC=1:9,推出AE:AC=1:3,即可解决问题.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AE}{AC}$)2,
∵S△ADE:S四边形DBCE=1:8,
∴S△ADE:S△ABC=1:9,
∴AE:AC=1:3,
∴AE:EC=1:2,
故选C.
点评 本题考查相似三角形的性质和判定、平行线的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,记住相似三角形的面积比等于相似比的平方,属于中考常考题型.

练习册系列答案
相关题目
12.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对肥城市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对肥城新闻栏目收视率的调查 | |
| D. | 对某校七年级(7)班同学身高情况的调查 |
9.若x1,x2是一元二次方程x2-3x+1=0的两个根,则x1+x2=( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
16.下列说法正确的是( )
| A. | 正有理数和负有理数统称为有理数 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 绝对值等于它的相反数的数是非正数 | |
| D. | 两数相加,和一定大于任何一个加数 |
6.如图将4个长、宽分别为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
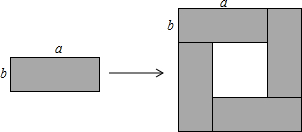

| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | 4ab=(a+b)2-(a-b)2 |
10.方程2-x=-2的解是( )
| A. | x=1 | B. | x=-4 | C. | x=4 | D. | x=0 |
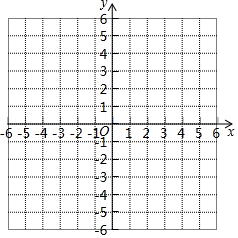 在平面直角坐标系中,点A(0,2),B(6,4).
在平面直角坐标系中,点A(0,2),B(6,4).