题目内容
16.某品牌服装店销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,该商店为了增加盈利,决定采取适当的降价措施,经市场调查发现,如果每件衬衫每降价4元,那么该商店平均每天可多卖出8件,(1)要想在销售这种衬衫上平均每天盈利1200元,那么每件衬衫应降价多少元?
(2)利用你所学的数学知识分析降价多少元利润最大,最大利润是多少?
分析 (1)根据题意可以列出相应的一元二次方程,从而可以解答本题;
(2)根据题意可以得到利润与降价之间的函数关系式,然后化为顶点式即可解答本题.
解答 解:(1)设每件衬衫应降价x元,
(40-x)(20+$\frac{x}{4}×8$)=1200,
解得,x1=10,x2=20,
即要想在销售这种衬衫上平均每天盈利1200元,那么每件衬衫应降价10元或20元;
(2)设每件衬衫降价x元,利润为w元,
w=(40-x)(20+$\frac{x}{4}×8$)=-2(x-15)2+1250,
∴当x=15时,利润最大,此时w=1250,
即降价15元利润最大,最大利润是1250元.
点评 本题考查二次函数的应用和一元二次方程的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用二次函数的顶点式求函数的最值.

练习册系列答案
相关题目
6.如图将4个长、宽分别为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
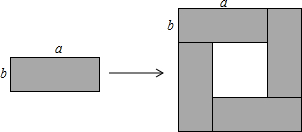

| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | 4ab=(a+b)2-(a-b)2 |
 已知△ABC的三个顶点的坐标分别为A(3,2),B(-4,0),C(0,7).
已知△ABC的三个顶点的坐标分别为A(3,2),B(-4,0),C(0,7).