题目内容
9.用恰当的方法解下列方程.(1)(x+3)(x-4)=-12;
(2)(2x-1)2-4(2x-1)=12.
分析 (1)首先去括号,进而分解因式得出即可.
(2)先移项,再把2x-1作为整体,分解因式即可求得.
解答 解:(1)(x+3)(x-4)=-12;
x2-x=0,
解得:x1=0,x2=1.
(2)(2x-1)2-4(2x-1)=12.
解:移项得,(2x-1)2-4(2x-1)-12=0,
分解因式得,(2x-1-6)(2x-1+2)=0,
即2x-7=0或2x+1=0,
解得x1=-$\frac{7}{2}$,x2=-$\frac{1}{2}$.
点评 本题考查了用因式分解法解一元二次方程,熟练掌握因式分解的方法是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
20.把一个正方形的一边增加2cm,另一边增加1cm,得到的矩形面积的2倍比正方形的面积多11cm2.设这个正方形的边长为x cm,依题意可得方程为( )
| A. | (x+2)(x+1)=2x2+14 | B. | 2(x+2)(x+1)=x2+11 | C. | 2(x-2)(x-1)=x2+11 | D. | (x-2)(x-1)=2x2+11 |
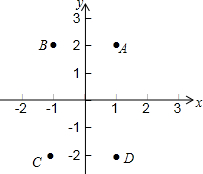 如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )
如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )
 在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.