题目内容
10.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | ($\frac{180}{n}$)° |
分析 (1)根据计算、观察,可发现规律:正n边形中的∠α=($\frac{180}{n}$)°;
(2)根据正n边形中的∠α=($\frac{180}{n}$)°,可得答案.
解答 解:(1)观察上面每个正多边形中的∠α,填写下表:
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | ($\frac{180}{n}$)° |
设存在正n边形使得∠α=21°,
得∠α=21°=($\frac{180}{n}$)°.
解得:n=8$\frac{4}{7}$,n是正整数,n=8$\frac{4}{7}$(不符合题意要舍去),
不存在正n边形使得∠α=21°.
点评 本题考查了多边形内角与外角,每题都利用了正多边形的内角:$\frac{(n-2)180°}{n}$,三角形的内角和定理,等腰三角形的两底角相等.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
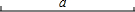 (1)如图,已知线段a,求作:以线段a为一边的等边三角形ABC(要求用尺规作图,保留作图痕迹).
(1)如图,已知线段a,求作:以线段a为一边的等边三角形ABC(要求用尺规作图,保留作图痕迹). 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,连接CD.若AC=3,AB=6,则∠BDC=120°.
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,连接CD.若AC=3,AB=6,则∠BDC=120°.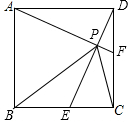 如图,在正方形ABCD中,点E、F分别为BC,CD的中点,则下列结论:①AF⊥DE;②AF=DE;③AD=BP;④PE+PF=$\sqrt{2}$PC.其中结论正确的有( )
如图,在正方形ABCD中,点E、F分别为BC,CD的中点,则下列结论:①AF⊥DE;②AF=DE;③AD=BP;④PE+PF=$\sqrt{2}$PC.其中结论正确的有( )