题目内容
18.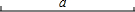 (1)如图,已知线段a,求作:以线段a为一边的等边三角形ABC(要求用尺规作图,保留作图痕迹).
(1)如图,已知线段a,求作:以线段a为一边的等边三角形ABC(要求用尺规作图,保留作图痕迹).(2)已知a+b=3,a-b=7,求ab的值.
分析 (1)首先作射线,再射线上截取AB=a,再分别以A、B为圆心,a长为半径画弧,两弧交于点C,再连接AC、BC即可.
(2)联立a+b=3,a-b=7,再解方程组,即可得到a、b的值,进而可得答案.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)$\left\{\begin{array}{l}{a+b=3}\\{a-b=7}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=5}\\{b=-2}\end{array}\right.$,
则ab=-10.
点评 此题主要考查了复杂作图,以及二元一次方程组的解法,关键是正确掌握做一条线段等于已知线段的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
 如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )
如图,在?ABCD中,∠B=50°,CE平分∠BCD,交AD于E,则∠DCE等于( )| A. | 25° | B. | 40° | C. | 50° | D. | 65° |
10.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.

(1)将下面的表格补充完整:
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | ($\frac{180}{n}$)° |
7.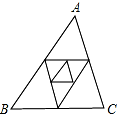 如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
 如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2014}}$ |
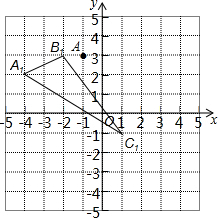 如图,已知△ABC平移后得到△A1B1C1,点A(-1,3)平移后得到A1(-4,2),
如图,已知△ABC平移后得到△A1B1C1,点A(-1,3)平移后得到A1(-4,2), 如图,⊙O的内接四边形ABCD中,∠A=45°,则∠C的度数135°.
如图,⊙O的内接四边形ABCD中,∠A=45°,则∠C的度数135°.