题目内容
2.证明:(1)有一个角是直角的菱形是正方形;
(2)对角线垂直的矩形是正方形.
分析 (1)由菱形的性质和已知条件得出AB=CD=BC=DA,四边形ABCD是矩形,得出∠A=∠B=∠C=∠D=90°,即可得出结论;
(2)由矩形的性质和已知条件得出∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形,得出AB=BC=CD=DA,即可得出结论.
解答 (1)如图1所示: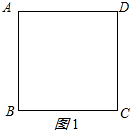 已知:四边形ABCD是菱形,∠A=90°;
已知:四边形ABCD是菱形,∠A=90°;
求证:四边形ABCD是正方形;
证明:∵四边形ABCD是菱形,∠A=90°,
∴AB=CD=BC=DA,四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是正方形;
(2)如图2所示:
已知:四边形ABCD是矩形,对角线AC⊥BD;
求证:四边形ABCD是正方形;
证明:∵四边形ABCD是矩形,对角线AC⊥BD,
∴∠BAD=∠ABC=∠BCD=∠CDA=90°,四边形ABCD是菱形,
∴AB=BC=CD=DA,
∴四边形ABCD是正方形.
点评 本题考查了菱形的性质与判定、矩形的性质与判定、正方形的判定方法;熟练掌握矩形和菱形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
10.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.

(1)将下面的表格补充完整:
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | ($\frac{180}{n}$)° |
17. 如图是自行车行驶路程与时间关系图,则整个行程过程的平均速度是( )
如图是自行车行驶路程与时间关系图,则整个行程过程的平均速度是( )
 如图是自行车行驶路程与时间关系图,则整个行程过程的平均速度是( )
如图是自行车行驶路程与时间关系图,则整个行程过程的平均速度是( )| A. | 15千米/时 | B. | 40千米/时 | C. | 25千米/时 | D. | 20千米/时 |
7.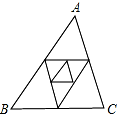 如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
 如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2014}}$ |
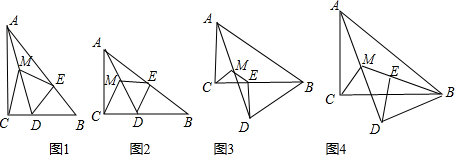
 如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为1cm2.
如图,△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为1cm2.