题目内容
20.某同学家计算多边形内角和时,得到的答案是1340°,老师指出他把某一个外角也加进去了,你能知道这个同学计算的是几边形的内角和吗?他多加的那个外角是多少度?分析 根据多边形的内角和公式(n-2)•180°可知,多边形的内角和是180°的倍数,然后求出多边形的边数以及多加的外角的度数即可得解.
解答 解:设多边形的边数为n,多加的外角度数为α,则
(n-2)•180°=1340°-α,
∵1340°=7×180°+80°,内角和应是180°的倍数,
∴同学多加的一个外角为80°,
∴这是7+2=9边形的内角和,
答:他计算的是9边形的内角和,他多加的那个外角是80度.
点评 本题考查了多边形的内角和公式,根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b;
③(3-x)(x+3)=x2-9;
④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2.
⑤(3-x)2=(x-3)2=x2-6x+9.
①(3a+4)(3a-4)=9a2-4;
②(2a2-b)(2a2+b)=4a2-b;
③(3-x)(x+3)=x2-9;
④(-x+y)(x+y)=-(x-y)(x+y)=-x2-y2.
⑤(3-x)2=(x-3)2=x2-6x+9.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.不等式组$\left\{\begin{array}{l}{2x-1>1}\\{4-2x≤0}\end{array}\right.$的解集是( )
| A. | x≤2 | B. | 1<x≤2 | C. | x>1 | D. | x≥2 |
10.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.

(1)将下面的表格补充完整:
| 正多边形边数 | 3 | 4 | 5 | 6 | … | n |
| ∠α的度数 | 60° | 45° | 36° | 30° | … | ($\frac{180}{n}$)° |
 如图,在⊙O中,弦AB⊥AC,AB=AC,OD⊥AB于D,OE⊥AC于E,若AC=2cm,则⊙O的半径为$\sqrt{2}$cm.
如图,在⊙O中,弦AB⊥AC,AB=AC,OD⊥AB于D,OE⊥AC于E,若AC=2cm,则⊙O的半径为$\sqrt{2}$cm.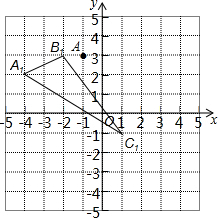 如图,已知△ABC平移后得到△A1B1C1,点A(-1,3)平移后得到A1(-4,2),
如图,已知△ABC平移后得到△A1B1C1,点A(-1,3)平移后得到A1(-4,2),