题目内容
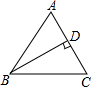 如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4.(1)求证:△BCD是直角三角形;
(2)求△ABC的面积.
考点:勾股定理的逆定理,等腰三角形的性质
专题:
分析:(1)利用勾股定理的逆定理即可直接证明△BCD是直角三角形;
(2)设AD=x,则AC=x+3,在直角△ABD中,利用勾股定理即可列出方程,解方程,即可求解.
(2)设AD=x,则AC=x+3,在直角△ABD中,利用勾股定理即可列出方程,解方程,即可求解.
解答:(1)证明:∵CD=3,BC=5,BD=4,
∴CD2+BD2=9+16=25=BC2,
∴△BCD是直角三角形,且∠BDC=90°;
(2)解:设AD=x,则AC=x+3.
∵AB=AC,
∴AB=x+3.
∵∠BDC=90°,
∴∠ADB=90°,
∴AB2=AD2+BD2,
即(x+3)2=x2+42,
解得:x=
,
∴AC=
+3=
,
∴S△ABC=
AC•BD=
×
×4=
.
∴CD2+BD2=9+16=25=BC2,
∴△BCD是直角三角形,且∠BDC=90°;
(2)解:设AD=x,则AC=x+3.
∵AB=AC,
∴AB=x+3.
∵∠BDC=90°,
∴∠ADB=90°,
∴AB2=AD2+BD2,
即(x+3)2=x2+42,
解得:x=
| 7 |
| 6 |
∴AC=
| 7 |
| 6 |
| 25 |
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 6 |
| 25 |
| 3 |
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.同时考查了勾股定理.

练习册系列答案
相关题目
已知函数y=kx+b(k,b是常数,k≠0),当x>5时,y<0;当x<5时,y>0,则y=kx+b的图象必经过点( )
| A、(0,5) |
| B、(5,0) |
| C、(-5,0) |
| D、(0,-5) |
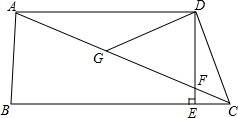 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
 已知几何体主视图和俯视图如图所示
已知几何体主视图和俯视图如图所示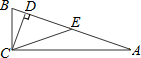 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数. 如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?
如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?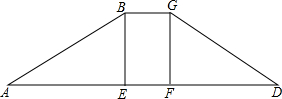 如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)
如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)