题目内容
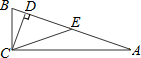 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.考点:直角三角形斜边上的中线,直角三角形的性质
专题:
分析:求出∠ACD=67.5°,∠BCD=22.5°,根据三角形内角和定理求出∠B=67.5°,根据直角三角形斜边上中线性质求出BE=CE,推出∠BCE=∠B=67.5°,代入∠ECD=∠BCE-∠BCD求出即可.
解答:解:∵∠ACD=3∠BCD,∠ACB=90°,
∴∠ACD=67.5°,∠BCD=22.5°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠B=180°-90°-22.5°=67.5°,
∵∠ACB=90°,E是斜边AB的中点,
∴BE=CE,
∴∠BCE=∠B=67.5°,
∴∠ECD=∠BCE-∠BCD=67.5°-22.5°=45°.
∴∠ACD=67.5°,∠BCD=22.5°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠B=180°-90°-22.5°=67.5°,
∵∠ACB=90°,E是斜边AB的中点,
∴BE=CE,
∴∠BCE=∠B=67.5°,
∴∠ECD=∠BCE-∠BCD=67.5°-22.5°=45°.
点评:本题考查了三角形内角和定理,直角三角形斜边上中线性质,等腰三角形的性质,直角三角形的性质的应用,解此题的关键是求出∠BCE和∠BCD的度数,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
 如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.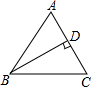 如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4. 如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC.
如图,已知:OE、OF分别是AB、AC的垂直平分线,∠OBC、∠OCB的平分线交于点P,求证:OP⊥BC. 如图,若∠1=∠2,则b
如图,若∠1=∠2,则b 如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=
如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=