题目内容
如图①,四边形ABCD中,AB∥CD,∠A=∠B,BC=CD=DA,图②是用多个同样的四边形密铺而成的,则∠A= °.


考点:平面镶嵌(密铺)
专题:
分析:先由AB∥CD,∠A=∠B可得四边形ABCD是等腰梯形,设等腰梯形的上底角为α,即∠C=∠D=α,则下底角为180°-α,即∠A=∠B=180°-α.由于用多个同样的四边形ABCD能够密铺,所以拼在同一顶点处的几个角能构成周角.观察图形,图②中顶点O处3个上底角的和为360°,即3α=360°,求出α的值即可.
解答:解: ∵AB∥CD,∠A=∠B,
∵AB∥CD,∠A=∠B,
∴四边形ABCD是等腰梯形.
设等腰梯形的上底角为α,即∠C=∠D=α,则下底角为180°-α,即∠B=180°-α.由题意得
3α=360°,解得α=120°,
∴∠A=180°-α=60°.
故答案为60.
 ∵AB∥CD,∠A=∠B,
∵AB∥CD,∠A=∠B,∴四边形ABCD是等腰梯形.
设等腰梯形的上底角为α,即∠C=∠D=α,则下底角为180°-α,即∠B=180°-α.由题意得
3α=360°,解得α=120°,
∴∠A=180°-α=60°.
故答案为60.
点评:本题考查了平面图形镶嵌(密铺),判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能.同时考查了等腰梯形的判定与性质.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
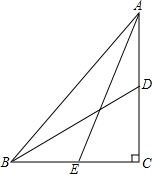 已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.
已知,在Rt△ABC中,∠C=90°,E、D分别为BC、AC中点,若AE=8,BD=6,求AB的值.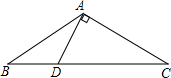 如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.
如图,在△ABC中,AB=AC,∠C=30°,DA⊥AB于点A.若BC=6cm,求BD的长.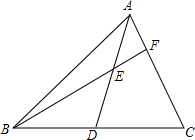 如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=
如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=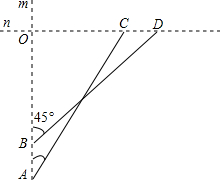 如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.(
如图,在一次速度测试中,互相垂直的两条轨道m,n上各有一部测试机甲和乙,某时刻甲在A处发现乙在其北偏东30°方向的C处,3min后,甲到达B处,且发现乙在其北偏东45°方向的D处,甲又继续行驶9min到达两条轨道的交叉点O处,已知甲、乙均为匀速行驶,甲的速度是30m/min,试求乙的速度.(
 如图,?ABCD中,E为CD中点,连接B、E两点与AD的延长线相交于点F,若AD=5,求DF的长.
如图,?ABCD中,E为CD中点,连接B、E两点与AD的延长线相交于点F,若AD=5,求DF的长.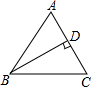 如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=3,BC=5,BD=4. 如图,GH交AB于N,交CD于P,交EF于M,PQ⊥GH交EF于Q,已知∠1=∠2=54°,∠4=36°,判断AB与EF的位置关系,并说明理由.
如图,GH交AB于N,交CD于P,交EF于M,PQ⊥GH交EF于Q,已知∠1=∠2=54°,∠4=36°,判断AB与EF的位置关系,并说明理由.