题目内容
2.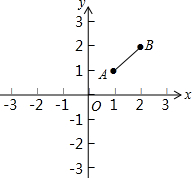 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),直线y=kx+3与线段AB有公共点,则k的取值范围是-2≤k≤-$\frac{1}{2}$.
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),直线y=kx+3与线段AB有公共点,则k的取值范围是-2≤k≤-$\frac{1}{2}$.
分析 当直线分别过点A、B时,可分别求出k值,再结合图形即可得出k的取值范围.
解答 解:当点A(1,1)在直线y=kx+3上时,
有1=k+3,
解得:k=-2;
当点B(2,2)在直线y=kx+3上时,
有2=2k+3,
解得:k=-$\frac{1}{2}$.
∴若直线y=kx+3与线段AB有公共点,则k的取值范围为-2≤k≤-$\frac{1}{2}$.
故答案为:-2≤k≤-$\frac{1}{2}$.
点评 本题考查了两条直线相交或平行问题以及一次函数图象上点的坐标特征,分别求出当直线过点A、B时k的值是解题的关键.

练习册系列答案
相关题目
13.已知一次函数y=kx-1,若y随x的增大而增大,则该函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.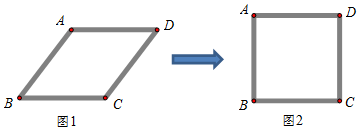 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )
小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )
 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )
小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )| A. | 20 cm | B. | 30 cm | C. | 40 cm | D. | $20\sqrt{2}$cm |
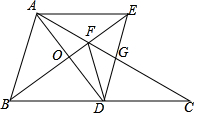 如图,在△ABC中,BC=2AB,AD是BC边上的中线,O是AD中点,过点A作AE∥BC,交BO的延长线于点E,BE交AC于点F,连接DE交AC于点G.
如图,在△ABC中,BC=2AB,AD是BC边上的中线,O是AD中点,过点A作AE∥BC,交BO的延长线于点E,BE交AC于点F,连接DE交AC于点G. 如图,点E是正方形ABCD内一点,将△BEC绕点C顺时针旋转90度至△DFC,若已知∠EBC=30°,∠BCE=80°,求∠F的度数.
如图,点E是正方形ABCD内一点,将△BEC绕点C顺时针旋转90度至△DFC,若已知∠EBC=30°,∠BCE=80°,求∠F的度数.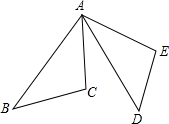 如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗?
如图,AB=AD,AC=AE,∠BAC=∠DAE,∠B与∠D相等吗? 如图,直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若∠A=36°,求∠DEF的度数.
如图,直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若∠A=36°,求∠DEF的度数. ,则x=________.
,则x=________.