题目内容
14.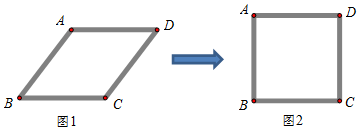 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )
小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得对角线AC=40cm,则图1中对角线AC的长为 ( )| A. | 20 cm | B. | 30 cm | C. | 40 cm | D. | $20\sqrt{2}$cm |
分析 如图1,2中,连接AC.在图2中,理由勾股定理求出BC,在图1中,只要证明△ABC是等边三角形即可解决问题.
解答 解:如图1,2中,连接AC.
在图2中,∵四边形ABCD是正方形,
∴AB=BC,∠B=90°,
∵AC=40°,
∴AB=BC=20$\sqrt{2}$,
在图1中,∵∠B=60°,BA=BC,
∴△ABC是等边三角形,
∴AC=BC=20$\sqrt{2}$,
故选D.
点评 本题考查菱形的性质、正方形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
4.下列命题,其中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两点之间,垂线段最短 | |
| C. | 图形的平移改变了图形的位置和大小 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
 如图,平行四边形ABCD的周长是38,对角线AC,BD相交于点O,△AOD与△AOB的周长之差是5,则AB的长是7.
如图,平行四边形ABCD的周长是38,对角线AC,BD相交于点O,△AOD与△AOB的周长之差是5,则AB的长是7.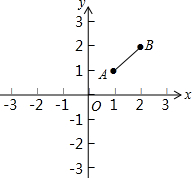 如图,在平面直角坐标系xOy中,A(1,1),B(2,2),直线y=kx+3与线段AB有公共点,则k的取值范围是-2≤k≤-$\frac{1}{2}$.
如图,在平面直角坐标系xOy中,A(1,1),B(2,2),直线y=kx+3与线段AB有公共点,则k的取值范围是-2≤k≤-$\frac{1}{2}$. OB.
OB.
 等( )
等( ) B.
B.  C.
C.  D.
D. 