题目内容
9.已知Rt△ABC中,∠C=90°,AC=3,BC=4,若以2为半径作⊙C,则斜边AB与⊙C的位置关系是( )| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
分析 根据题意可求得直角三角形斜边上的高,再根据直线和圆的位置关系,判断圆心到直线AB的距离与2的大小关系,从而确定⊙C与AB的位置关系.
解答 解:由勾股定理得AB=5,再根据三角形的面积公式得,3×4=5×斜边上的高,
∴斜边上的高=$\frac{12}{5}$,
∵$\frac{12}{5}$>2,
∴⊙C与AB相离.
故选:C.
点评 本题考查了直线和园的位置关系,解决的根据是直线和圆相离?圆心到直线的距离大于圆的半径.

练习册系列答案
相关题目
19.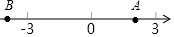 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
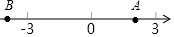 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丁 |
20.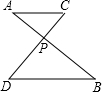 如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
 如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )| A. | ∠APD=39° | B. | ∠APD=50° | C. | ∠APD=89° | D. | ∠APD=76° |
17.下列计算正确的是( )
| A. | x4+x4=2x8 | B. | (x2y)3=x6y | C. | -(x2)3=x5 | D. | -x3•(-x)5=x8 |
14.若-2是关于x的方程3x+4=$\frac{x}{2}$-a的解,则a2017的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2017 |
1.下面合并同类项正确的是( )
| A. | 3x+2x2=5x3 | B. | 2a2b-2a2b-a2b=1 | C. | -ab-ab=0 | D. | -xy2+xy2=0 |
18. 如图,数轴上点A,B所对应的实数分别是1和$\sqrt{2}$,点B与点C关于点A对称,则点C所对应的实数是( )
如图,数轴上点A,B所对应的实数分别是1和$\sqrt{2}$,点B与点C关于点A对称,则点C所对应的实数是( )
 如图,数轴上点A,B所对应的实数分别是1和$\sqrt{2}$,点B与点C关于点A对称,则点C所对应的实数是( )
如图,数轴上点A,B所对应的实数分别是1和$\sqrt{2}$,点B与点C关于点A对称,则点C所对应的实数是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | $\sqrt{2}$-1 |
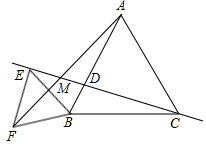 如图,等边△ABC中,点D是AB上一点,点E在线段CD延长线上,以BE为一边且在BE的左侧作等边△BEF,连接AF.
如图,等边△ABC中,点D是AB上一点,点E在线段CD延长线上,以BE为一边且在BE的左侧作等边△BEF,连接AF.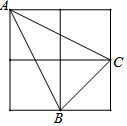 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )
如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形的个数有(不包含△ABC本身)( )