题目内容
12. 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 先写出A点坐标,则利用两直线平行的问题,设直线l2对应的函数表达式为y=2x+b,再把A点坐标代入求出b的值,则可确定B点坐标,于是可得到OB的长.
解答 解:∵OA=2,
∴A(-2,0),
∵l1∥l2,直线l1对应的函数表达式为y=2x,
∴直线l2对应的函数表达式可设为y=2x+b,
把A(-2,0)代入得-4+b=0,解得b=4,
∴直线l2对应的函数表达式为y=2x+4,
∴B(0,4),
∴OB=4.
故选B
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.下列去括号中,正确的是( )
| A. | -(x-y+z)=-x+y-z | B. | x+2(y-z)=x+2y-z | ||
| C. | ${a^2}-\frac{3}{4}(a+2)={a^2}-\frac{3}{4}a+\frac{3}{2}$ | D. | a-(x-y+z)=a-x+y+z |
3.一个正多边形每一个外角为36°,则这个多边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
17.人体中成熟的红细胞的平均直径为0.000 007 7m,将0.000 007 7用科学记数法表示为( )
| A. | 7.7×10-5 | B. | 77×10-6 | C. | 77×10-5 | D. | 7.7×10-6 |
1.已知点(-4,y1),(2,y2)都在直线y=-2x+3上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
 如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.
如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.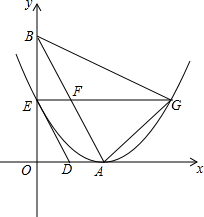 如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.
如图,直线y=-$\sqrt{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,点B,两动点D,E分别从点A,点B同时出发向点O运动(运动到点O停止),运动速度分别是1个单位长度/秒和$\sqrt{3}$个单位长度/秒,设运动时间为t秒,以点A为顶点的抛物线经过点E,过点E作x轴的平行线,与抛物线的另一个交点为点G,与AB相交于点F.