题目内容
7.如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

分析 (1)利用等角的余角相等即可证明.
(2)①只要证明∠CEF=∠CFE即可.
②由△DCA∽△DBC,得$\frac{DC}{DB}$=$\frac{AC}{BC}$=$\frac{DA}{CD}$=$\frac{3}{4}$,再由△DCE∽△DBF,得$\frac{EC}{BF}$=$\frac{DC}{DB}$,设EC=CF=x,列出方程即可解决问题.
解答 (1)证明:如图1中,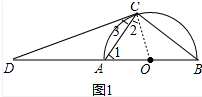 连接OC.
连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴$\frac{DC}{DB}$=$\frac{AC}{BC}$=$\frac{DA}{CD}$=$\frac{3}{4}$,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴$\frac{EC}{FB}$=$\frac{DC}{DB}$=$\frac{3}{4}$,设EC=CF=x,
∴$\frac{x}{4-x}$=$\frac{3}{4}$,
∴x=$\frac{12}{7}$.
∴CE=$\frac{12}{7}$.
点评 本题考查切线的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,学会用方程的思想思考问题,属于中考常考题型.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | ∠B=80° | B. | ∠C=80° | C. | ∠D=80° | D. | 以上都错误 |
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
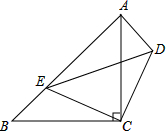 如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.
如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.