题目内容
4. 如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.
如图,把一张长方形纸片折叠,如果∠2=64°,那么∠1=58°.
分析 由于四边形ABCD是矩形,那么AD∥BC,利用两直线平行内错角相等,可知∠2=∠4,再根据折叠的性质可知∠1=∠3,根据平角的定义可知∠1+∠3+∠4=180°,从而易求∠1.
解答  解:如右图所示,
解:如右图所示,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠2=∠4,
又∵∠1折叠后与∠3重合,
∴∠1=∠3,
又∵∠1+∠3+∠4=180°,
∴2∠1=180°-64°=116°,
∴∠1=58°,
故答案为58°.
点评 本题考查了矩形的性质、平行线的性质、平角定义、折叠的性质.关键是能看出∠1=∠3.

练习册系列答案
相关题目
14.如图图形中,是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )
 如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )
如图,在平面直角坐标系中,直线l1对应的函数表达式为y=2x,将直线l1向左平移,使之分别与x、y轴交于点A、B,若OA=2,则线段OB的长为( )| A. | 3 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
19.为了了解我区初一年级学生的身高情况,抽查了1000名学生的身高进行统计分析.所抽查的1000名学生的身高是这个问题的( )
| A. | 总体 | B. | 个体 | C. | 样本 | D. | 样本容量 |
9.若分式$\frac{x}{x-3}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≠3 | C. | x≠-3 | D. | x≠±3 |
13.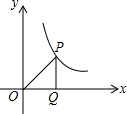 如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
 如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )
如图,点P在反比例函数y=$\frac{k}{x}$(x>0)第一象限的图象上,PQ垂直x轴,垂足为Q,设△POQ的面积是s,那么s与k之间的数量关系是( )| A. | $s=\frac{k}{4}$ | B. | $s=\frac{k}{2}$ | C. | s=k | D. | 不能确定 |
14.点A(-3,-2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )
| A. | (1,0) | B. | (1,-4) | C. | (-1,0) | D. | (-5,-1) |