题目内容
1．已知点（-4，y1），（2，y2）都在直线y=-2x+3上，则y1，y2大小关系是（ ）| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不能比较 |
分析 直接把点（-4，y1），（2，y2）代入直线y=-2x+3，求出y1，y2的值，再比较其大小即可．
解答 解：∵点（-4，y1），（2，y2）在直线y=-2x+3上，
∴y1=8+3=11，y2=-4+3=-1，
∵11＞-1，
∴y1＞y2．
故选A．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
孟建平名校考卷系列答案
相关题目
11．某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如表：
其中a为常数，且3≤a≤5
（1）若产销甲、乙两种产品的年利润分别为y1万元、y2万元，直接写出y1、y2与x的函数关系式；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
| 产品 | 每件售价（万元） | 每件成本（万元） | 每年其他费用（万元） | 每年最大产销量（件） |
| 甲 | 6 | a | 20 | 200 |
| 乙 | 20 | 10 | 40+0.05x2 | 80 |
（1）若产销甲、乙两种产品的年利润分别为y1万元、y2万元，直接写出y1、y2与x的函数关系式；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
12．
如图，在平面直角坐标系中，直线l1对应的函数表达式为y=2x，将直线l1向左平移，使之分别与x、y轴交于点A、B，若OA=2，则线段OB的长为（ ）
如图，在平面直角坐标系中，直线l1对应的函数表达式为y=2x，将直线l1向左平移，使之分别与x、y轴交于点A、B，若OA=2，则线段OB的长为（ ）| A． | 3 | B． | 4 | C． | 2$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
9．若分式$\frac{x}{x-3}$有意义，则x满足的条件是（ ）
| A． | x≠0 | B． | x≠3 | C． | x≠-3 | D． | x≠±3 |
13．
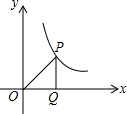如图，点P在反比例函数y=$\frac{k}{x}$（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（ ）
如图，点P在反比例函数y=$\frac{k}{x}$（x＞0）第一象限的图象上，PQ垂直x轴，垂足为Q，设△POQ的面积是s，那么s与k之间的数量关系是（ ）| A． | $s=\frac{k}{4}$ | B． | $s=\frac{k}{2}$ | C． | s=k | D． | 不能确定 |
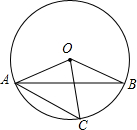如图，在⊙O中，AB是弦，C是$\widehat{AB}$上一点．若∠OAB=25°，∠OCA=40°，则∠BOC的大小为30度．