题目内容
4.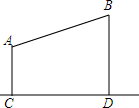 因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?
因需要,计划在山顶A,B处架绳索设一绳索滑道.已测到山顶A的海拔高度AC为300米,山顶B的海拔高度BD为800米,山顶A,B之间的水平宽度CD为1200米,问这一绳索至少需要多少米?
分析 作AE⊥BD于E,根据矩形的性质得到AE=CD、DE=AC,根据勾股定理计算得到答案.
解答 解: 作AE⊥BD于E,
作AE⊥BD于E,
由题意得,四边形ACDE为矩形,
BE=BD-DE=BD-AC=500米,又AE=CD=1200米,
由勾股定理得,AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=1300米,
答:这一绳索至少需要1300米.
点评 本题考查的是勾股定理的应用,正确作出辅助线、构造直角三角形是解题的关键,注意矩形的性质的灵活运用和勾股定理的运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
16.已知a+b=5,ab=4,则ab2+a2b-a-b的值是( )
| A. | -15 | B. | 15 | C. | 6 | D. | -6 |
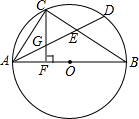 AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF.
AB是⊙O的直径,D是$\widehat{AB}$上的一点,C是$\widehat{AD}$的中点,AD,BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:①CG=EG=AG;②AD=2CF. 如图,0A、0B都是⊙0的半径,∠A0B=100°,异于A、B的动点C在⊙0上,求∠ACB的度数.
如图,0A、0B都是⊙0的半径,∠A0B=100°,异于A、B的动点C在⊙0上,求∠ACB的度数. 如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.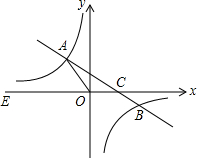 如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数的图象y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,线段OA=5,OC=3,E为x轴上一点,且tan∠AOE=$\frac{4}{3}$.