题目内容
8.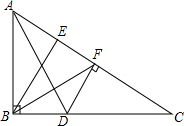 如图,在Rt△ABC中,∠ABC=90°,BE⊥AC,垂足为点E,AD平分∠BAC,DF∥BE,EF=4,求点F到BC的距离.
如图,在Rt△ABC中,∠ABC=90°,BE⊥AC,垂足为点E,AD平分∠BAC,DF∥BE,EF=4,求点F到BC的距离.
分析 作FH⊥BC于H,根据角平分线的性质得到DF=DB,证明∠DBF=∠DFB,根据平行线的性质得到∠EBF=∠DFB,根据角平分线的性质得到答案.
解答 解:作FH⊥BC于H,
∵DF∥BE,BE⊥AC,
∴DF⊥AC,
∵AD平分∠BAC,∠ABC=90°,DF⊥AC,
∴DF=DB,
∴∠DBF=∠DFB,
∵DF∥BE,
∴∠EBF=∠DFB,
∴∠EBF=∠DBF,BE⊥AC,FH⊥BC,
∴FH=EF=4.
点评 本题考查的是角平分线的性质和平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知a+b=5,ab=4,则ab2+a2b-a-b的值是( )
| A. | -15 | B. | 15 | C. | 6 | D. | -6 |
3.下列变形中正确的是( )
| A. | $\frac{5a}{3b}$=$\frac{25{a}^{2}}{9{b}^{2}}$ | B. | -$\frac{c}{-a+b}$=$\frac{c}{a+b}$ | ||
| C. | $\frac{6a-5}{7-b}$=$\frac{5-6a}{b-7}$ | D. | $\frac{a-b}{a}$=$\frac{{a}^{2}-{b}^{2}}{a(a+b)}$ |
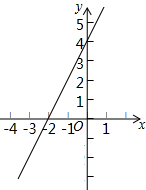 如图所示,直线l是一次函数的图象.
如图所示,直线l是一次函数的图象. 如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.
如图,在△ABC中,AB=5,AC=3,D是BC的中点,AD=2,求△ABC的面积.