题目内容
2. 已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.
已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.
分析 根据平行线的性质和角平分线定义求出∠EDB=∠EBD,推出DE=BE,设DE=BE=x,证相似,得出比例式,代入求出即可.
解答 解:∵DE∥BC,
∴∠EDB=∠CBD,
∵BD是∠ABC的角平分线,
∴∠CBD=∠ABD,
∴∠EDB=∠EBD,
∴DE=BE,
设DE=BE=x,
∵DE∥BC,
∴△AED∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$,
∴$\frac{x}{8}=\frac{4}{x+4}$,
解得:x=4,(负值舍去),
∴DE=4.
点评 本题考查了等腰三角形的性质和判定,平行线的性质,相似三角形的性质和判定的应用,解此题的关键是求出BE=DE和求出△AED∽△ABC.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
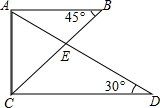 将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{{{S_{△ABE}}}}{{{S_{△ACE}}}}$=$\frac{\sqrt{3}}{3}$.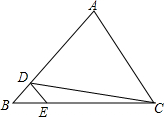 如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )