题目内容
12.抛物线y=x2-2x+c的顶点在直线y=-2x+1上,则抛物线与y轴交点的坐标为(0,0).分析 根据题意可知顶点即为抛物线和直线的交点,所以把对称轴x=1代入y=-2x+1,即可求得顶点坐标,进一步代入抛物线解析式,求得c得出答案即可.
解答 解:∵抛物线y=x2-2x+c的对称轴x=1,顶点在直线y=-2x+1上,
∴顶点即为抛物线和直线的交点,
把x=1代入y=-2x+1,得y=-1,
∴抛物线顶点坐标为(1,-1),
∴-1=1-2+c,
∴c=0,
∴抛物线与y轴交点的坐标为(0,0).
故答案为:(0,0).
点评 本题考查了二次函数的性质,掌握抛物线对称轴与交点坐标的求法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.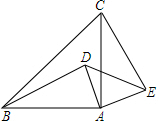 如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
(1)探索BD与CE的数量关系与位置关系;
(2)如果把△ADE绕点A旋转一周,则有哪些具有代表性的图形,请画出,并选择其中一种说明理由.
 如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.
如图,△ABC与△ADE均是等腰直角三角形,连接BD、CE.(1)探索BD与CE的数量关系与位置关系;
(2)如果把△ADE绕点A旋转一周,则有哪些具有代表性的图形,请画出,并选择其中一种说明理由.

1.科研人员在测试一枚火箭竖直向上升空时发现,火箭的高度h(m)与时间t(s)的关系数据如下:
(1)根据上表,以时间t为横轴,高度h为纵轴建立直角坐标系,并描出上述各点;
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
| 时间t/s | 1 | 5 | 10 | 15 | 20 | 25 |
| 火箭高度h/m | 155 | 635 | 1010 | 1135 | 1010 | 635 |
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗?
(3)请由以上数据确定h与t的函数表达式;
(4)你能由上述三种函数的表示方式求出该火箭的最高射程是多少吗?你是根据哪种表示方式求解的?
 已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长.
已知:如图,BD是△ABC的角平分线,DE∥BC,点E在AB上,AE=4,BC=8,求DE的长. 如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积.
如图,平面直角坐标系中,已知△ABC中,A(1,3),B(2,2),C(6,5),求△ABC的面积. 如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数.
如图,在五边形ABCDE中,AB∥CD,∠A=125°,∠D=150°,求∠E的度数.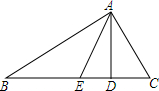 如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.
如图,在△ABC中,AD⊥BC与点D,AE平分∠BAC,若∠B=40°,∠C=60°,求∠EAD的度数,并直接写出∠EAD和∠B,∠C间的关系,不需证明.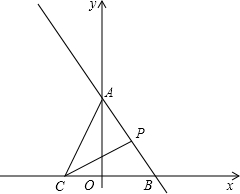 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,若点P是l上一动点,点N在坐标轴上,当以A,C,P,N为顶点的四边形是平行四边形时,求点P,N的坐标.