题目内容
 如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=考点:三角形中位线定理,三角形内角和定理
专题:
分析:首先,利用三角形内角和定理求得∠AED=70°;然后根据三角形中位线定理推知DE∥BC,∠C=∠AED.
解答:解:如图,∵在△AED中,∠A=50°,∠ADE=60°,
∴∠AED=70°.
又∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠C=∠AED=70°.
故答案是:70°.
∴∠AED=70°.
又∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
∴∠C=∠AED=70°.
故答案是:70°.
点评:本题考查了三角形中位线定理和三角形内角和定理.解题时,要挖掘出隐含在题干中的已知条件:三角形内角和是180度.

练习册系列答案
相关题目
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”,若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,则b的值( )
| A、±2 | B、±3 | C、2 | D、3 |
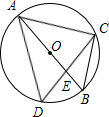 如图,AB是⊙O的直径,△ACD为正三角形,则∠BAC=
如图,AB是⊙O的直径,△ACD为正三角形,则∠BAC= 图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=
图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM= 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是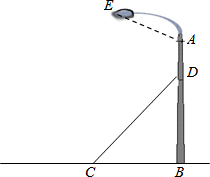 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.