题目内容
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”,若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,则b的值( )
| A、±2 | B、±3 | C、2 | D、3 |
考点:抛物线与x轴的交点
专题:新定义
分析:把抛物线三角形系数代入抛物线,令y=0求出点A的坐标,再求出顶点坐标,然后根据等腰直角三角形的斜边上的高线等于斜边的一半列出方程求解即可得到b的值.
解答:解:∵抛物线三角形系数为[-1,b,0],
∴抛物线解析式为y=-x2+bx=-(x-
)2+
,
∴顶点坐标为(
,
),
令y=0,则-x2+bx=0,
解得x1=0,x2=b,
∴与x轴的交点为(0,0),(b,0),
∵“抛物线三角形”是等腰直角三角形,
∴
=
|b|,
∴b2=2b或b2=-2b,
∵b=0时,抛物线与x轴只有一个交点(0,0),
∴b=0不符合题意,
∴b=2或b=-2,
故选:A.
∴抛物线解析式为y=-x2+bx=-(x-
| b |
| 2 |
| b2 |
| 4 |
∴顶点坐标为(
| b |
| 2 |
| b2 |
| 4 |
令y=0,则-x2+bx=0,
解得x1=0,x2=b,
∴与x轴的交点为(0,0),(b,0),
∵“抛物线三角形”是等腰直角三角形,
∴
| b2 |
| 4 |
| 1 |
| 2 |
∴b2=2b或b2=-2b,
∵b=0时,抛物线与x轴只有一个交点(0,0),
∴b=0不符合题意,
∴b=2或b=-2,
故选:A.
点评:本题主要考查了等腰直角三角形的性质,待定系数法求二次函数解析式,读懂题目信息,理解“抛物线三角形”的定义是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
PM2.5是指大气中直径小于或等于0.000000025米的可吸入颗粒物,也称可吸入肺颗粒物,对人体的健康有危害.0.000000025米用科学记数法应记为( )
| A、0.25×10-7 |
| B、2.5×10-8 |
| C、2.5×10-9 |
| D、25×10-8 |
当m<-1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是( )
| A、两负根 |
| B、两异号根,且正根的绝对值较大 |
| C、两正根 |
| D、两异号根,且负根的绝对值较大 |
 如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=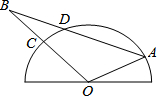 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为