题目内容
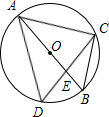如图，AB是⊙O的直径，△ACD为正三角形，则∠BAC=考点：圆周角定理,等边三角形的性质
专题：
分析：根据△ACD为正三角形，求出∠D=60°，再根据∠B=∠D，判断出∠B=60°，根据直径所对的圆周角是90°，在直角三角形中求出∠BAC的值．
解答：解：∵△ACD为正三角形，
∴∠D=60°，
∴∠B=∠D=60°，
∵AB是⊙O直径，
∴∠ACB=90°，
∴∠BAC=90°-60°=30°．
故答案为30°．
∴∠D=60°，
∴∠B=∠D=60°，
∵AB是⊙O直径，
∴∠ACB=90°，
∴∠BAC=90°-60°=30°．
故答案为30°．
点评：本题考查了圆周角定理，利用正三角形的性质、同弧所对的圆周角相等进行解答．
练习册系列答案
相关题目
如图，已知△ABC，以AC为直径的⊙O交AB于点D，点E为弧
如图，已知直线l：y=-x+2与y轴交于点A，抛物线y=（x-1）2+k经过点A，其顶点为B，另一抛物线y=（x-h）2+2-h（h＞1）的顶点为D，两抛物线相交于点C，
在正方形网格中，△ABC如图放置，则sinB的值为
如图，数轴上M、N两点表示的数分别为
如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C=