题目内容
5.算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )| A. | 4 | B. | 2 | C. | 8 | D. | 6 |
分析 先配一个(2-1),则可利用平方差公式计算出原式=264,然后利用底数为2的正整数次幂的个位数的规律求解.
解答 解:原式=(2-1)(2+1)×(22+1)×(24+1)×…×(232+1)+1
=(22-1)×(22+1)×(24+1)×…×(232+1)+1
=(24-1)×(24+1)×…×(232+1)+1
=(232-1)×(232+1)+1
=264-1+1
=264,
因为21=2,22=4,23=8,24=16,25=32,
所以底数为2的正整数次幂的个位数是2、4、8、6的循环,
所以264的个位数是6.
故选D.
点评 本题考查了平方差公式:两个数的和与这两个数的差相乘,等于这两个数的平方差,即(a+b)(a-b)=a2-b2.

练习册系列答案
相关题目
 在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.
在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.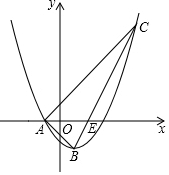 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.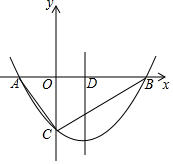 定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.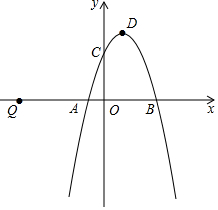 如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.
如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1. 如图,平面镜A与B之间夹角(∠AOB)为150°,光线经过平面镜A反射后射在平面镜B上,再反射出去.若∠1=∠2,则∠1=15度.
如图,平面镜A与B之间夹角(∠AOB)为150°,光线经过平面镜A反射后射在平面镜B上,再反射出去.若∠1=∠2,则∠1=15度.