题目内容
15. 在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.
在一个可以改变体积的密闭容器内,装有一定质量的二氧化碳.当改变容器的体积时,气体的密度也会随之改变,密度ρ是体积V的反比例函数,它的图象如图所示.(1)求密度ρ(单位:㎏/m3)与体积V(单位:m3)之间的函数关系式;
(2)求V=9时,二氧化碳的密度ρ.
分析 (1)设密度ρ(单位:kg/m3)与体积V(单位:m3)的反比例函数解析式为ρ=$\frac{k}{V}$,把点(5,2)代入解析式根据待定系数法即可求得;
(2)把V=9代入解析式即可求出二氧化碳的密度.
解答 解:(1)设密度ρ与体积V的反比例函数解析式为ρ=$\frac{k}{V}$,把点(5,2)代入解ρ=$\frac{k}{V}$,得k=10,
∴密度ρ与体积V的反比例函数解析式为ρ=$\frac{10}{V}$,V>0.
(2)把V=9代入ρ=$\frac{10}{V}$,得ρ=$\frac{10}{9}$kg/m3.
点评 现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
6.购买单价为a元的练习本2本和b支单价是3元的圆珠笔,则总价是( )元.
| A. | a+b | B. | 2a+b | C. | 2a+3b | D. | a+3b |
3.关于x的不等式组$\left\{\begin{array}{l}x>a\\ x>2-a\end{array}\right.$的解集是x>a,则a的取值范围是( )
| A. | a>1 | B. | a≤1 | C. | a≥1 | D. | a<1 |
10.方程4x-1=3的解是( )
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
20.下列各组数中,互为相反数的是( )
| A. | 2与$\frac{1}{2}$ | B. | -1与(-1)2 | C. | (-1)2与1 | D. | 2与|-2| |
7.下列合并同类项中正确的是( )
| A. | 5xy-xy=5 | B. | m+m=m2 | C. | -y-y=0 | D. | -2xy+2xy=0 |
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )
| A. | (4,-2) | B. | (-4,2) | C. | (-2,-4) | D. | (2,4) |
5.算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )
| A. | 4 | B. | 2 | C. | 8 | D. | 6 |
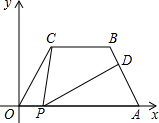 如图,平面直角坐标系中,在四边形OABC中,BC∥OA,OC=AB,OA=7,AB=4,∠COA=60°,点P是x轴上一个动点,点P不与点O、A重合,连接CP,点D是边AB上一点,连接PD.
如图,平面直角坐标系中,在四边形OABC中,BC∥OA,OC=AB,OA=7,AB=4,∠COA=60°,点P是x轴上一个动点,点P不与点O、A重合,连接CP,点D是边AB上一点,连接PD.