题目内容
2.已知⊙O的半径r=2,圆心O到直线l的距离d是方程x2-5x+6=0的解,则直线l与⊙O的位置关系是( )| A. | 相切 | B. | 相交 | C. | 相切或相交 | D. | 相切或相离 |
分析 先解方程,根据距离d与r的大小关系得出:直线与圆的位置关系.
解答 解:x2-5x+6=0,
(x-3)(x-2)=0,
x=3或2,
当d=3时,则d>r,所以直线l与⊙O的位置关系是相离;
当d=2时,则d=r,所以直线l与⊙O的位置关系是相切;
则直线l与⊙O的位置关系是:相切或相离;
故选D.
点评 本题考查了一元二次方程的解法及直线与圆的位置关系,判断直线和圆的位置关系时:设⊙O的半径为r,圆心O到直线l的距离为d,①直线l和⊙O相交?d<r;②直线l和⊙O相切?d=r;③直线l和⊙O相离?d>r.

练习册系列答案
相关题目
17.若关于x的不等式3-x>a的解集为x<4,则关于m的不等式2m+3a<1的解为( )
| A. | m<2 | B. | m>1 | C. | m>-2 | D. | m<-1 |
17.在下列条件中,不能说明△ABC≌△A′B′C′的是( )
| A. | ∠C=∠C′,AC=A′C′,BC=B′C′ | B. | ∠B=∠B′,∠C=∠C′,AB=A′B′ | ||
| C. | ∠A=∠A′,AB=A′B′,BC=B′C′ | D. | AB=A′B′,BC=B′C′,AC=A′C |
11.下列各式中,不正确的是( )
| A. | 5$\sqrt{a}$-3$\sqrt{a}$=2$\sqrt{a}$ | B. | $\sqrt{1\frac{9}{16}}$=1$\frac{3}{4}$ | C. | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{3}$+$\sqrt{2}$=$\frac{1}{\sqrt{3}-\sqrt{2}}$ |
12. 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
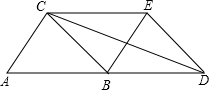 如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.
如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.