题目内容
12．
如图，⊙O的半径为5，AB为⊙O的弦，OC⊥AB于点C．若OC=3，则弦AB的长为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
分析 连接OA，先根据勾股定理求出AC的长，再由垂径定理可知AB=2AC，故可得出结论．
解答 
解：连接OA，
∵OC⊥AB，OA=5，OC=3，
∴AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=4，
∵OC过圆心，
∴AB=2AC=2×4=8．
故选C．
点评 本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
2．已知⊙O的半径r=2，圆心O到直线l的距离d是方程x2-5x+6=0的解，则直线l与⊙O的位置关系是（ ）
| A． | 相切 | B． | 相交 | C． | 相切或相交 | D． | 相切或相离 |
3．已知下列结论：①4的平方根是2；②平方根等于本身的数只有0；③$\frac{\sqrt{3}}{2}$是分数；④数轴上的所有点都表示的是有理数．其中正确的说法的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
20．下列运用完全平方公式计算正确的是（ ）
| A． | （m-1）2=m2-1 | B． | （2a+b）2=2a2+2ab+b2 | ||
| C． | （x2-$\frac{1}{2}$）2=x4-x2+$\frac{1}{4}$ | D． | 3（m+1）2=3m2+2m+1 |
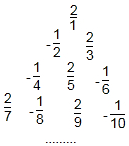将分数：$\frac{2}{1}$，-$\frac{1}{2}$，$\frac{2}{3}$，-$\frac{1}{4}$，$\frac{2}{5}$，-$\frac{1}{6}$，$\frac{2}{7}$，-$\frac{1}{8}$，$\frac{2}{9}$，…．将这列数排成如图形式：
1．|-$\frac{3}{4}$|的相反数是（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | -$\frac{4}{3}$ |
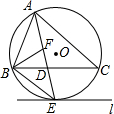如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．