题目内容
14.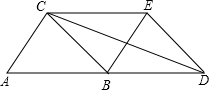 如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.
如图,平移△ABC到△BDE的位置,且点D在边AB的延长线上,连接EC,CD,若AB=BC,那么在以下四个结论:①四边形ABEC是平行四边形;②四边形BDEC是菱形;③AC⊥DC;④DC平分∠BDE,正确的有①②③④.
分析 先证明四边形ABEC是平行四边形,再求证四边形BDEC为菱形,根据菱形的对角线即角平分线性质可以解决题目.
解答 解:∵△BDE是△ABC平移过去的,且A、D三点一线,
∴AD∥CE,AC∥BE,
∴四边形ABEC为平行四边形,故①命题正确;
∵AB=BD,且AB=BC,
∴AB=BD=DE=EC=BC,即四边形BDEC为菱形,故②命题正确;
∵菱形对角线垂直,∴BE⊥CD,
∵AC∥BE,∴AC⊥CD,故③命题正确;
∵菱形的对角线即角平分线,且四边形BDEC为菱形,
∴DC为∠BDE的角平分线,故④命题正确.
故答案为:①②③④.
点评 本题考查的是根据平行四边形,菱形的定义判定四边形,要求学生掌握菱形对角线即角平分线且互相垂直的性质.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
5.若a+b=-5,c=2,则-ac-bc等于( )
| A. | 10 | B. | -10 | C. | 3 | D. | -3 |
2.已知⊙O的半径r=2,圆心O到直线l的距离d是方程x2-5x+6=0的解,则直线l与⊙O的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相切或相交 | D. | 相切或相离 |
9.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1)剩余部分虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )cm2
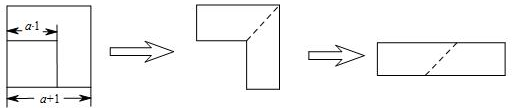

| A. | 2 | B. | 2a | C. | 4a | D. | (a2-1) |
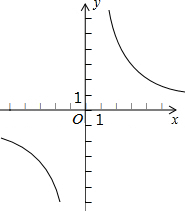 反比例函数y=$\frac{k}{x}$(k≠0)过A(3,4),点B与点A关于直线y=2对称,抛物线y=-x2+bx+c过点B和C(0,3).
反比例函数y=$\frac{k}{x}$(k≠0)过A(3,4),点B与点A关于直线y=2对称,抛物线y=-x2+bx+c过点B和C(0,3).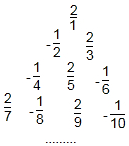 将分数:$\frac{2}{1}$,-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{1}{4}$,$\frac{2}{5}$,-$\frac{1}{6}$,$\frac{2}{7}$,-$\frac{1}{8}$,$\frac{2}{9}$,….将这列数排成如图形式:
将分数:$\frac{2}{1}$,-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{1}{4}$,$\frac{2}{5}$,-$\frac{1}{6}$,$\frac{2}{7}$,-$\frac{1}{8}$,$\frac{2}{9}$,….将这列数排成如图形式: