题目内容
19.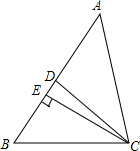 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
分析 在△BCE中由∠BEC=90°,∠B=60°能够得出∠BCE=30°;结合CD是∠ACB的角平分线,∠DCE=10°可得出∠ACE的度数;在Rt△ACE中由∠ACE的度数及∠AEC=90°,即可得出∠A的度数.
解答 解: ∵CE是AB边上的高,
∵CE是AB边上的高,
∴∠A+∠ACE=90°,∠B+∠BCE=90°.
∵CD是∠ACB的角平分线,
∴∠ACD=∠BCD=$\frac{1}{2}$∠ACB,
又∵∠DCE=10°,∠B=60°,
∴∠BCE=90°-∠B=30°,∠BCD=∠BCE+∠DCE=40°,
∴∠ACE=∠ACD+∠DCE=∠BCD+∠DCE=50°,
∴∠A=90°-∠ACE=40°.
点评 本题考查了三角形的内角和、三角形的角平分线及高线,解题的关键是找出∠ACB一半的度数.本题属于基础题,难度不大,解决该类型题目时,利用角平分线及三角形的内角和找到相关角的大小是关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.下列个数中,不是无理数的是( )
| A. | 0.$\stackrel{.}{5}$ | B. | $\sqrt{7}$ | C. | π | D. | 0.151151115… |
4.下列各组数中,属于勾股数的是( )
| A. | 2.5,6,6.5 | B. | 5,7,10 | C. | $\sqrt{2},\sqrt{3},\sqrt{5}$ | D. | 6,8,10 |
11.某市的中考各科试卷总分为600分,其中数学为120分,若用扇形统计图画出各科分数比例,则数学所占扇形圆心角为( )度.
| A. | 90 | B. | 45 | C. | 120 | D. | 72 |
9.已知一次函数y=2x+2与x轴y轴分别交于A、B两点,另一直线y=kx+3交x轴正半轴于E、交y轴于F点,如△AOB与E、F、O三点组成的三角形相似,那么k值为( )
| A. | -0.5 | B. | -2 | C. | -0.5或-2 | D. | 以上都不对 |
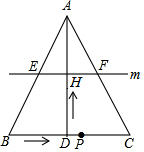 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).当t=$\frac{280}{183}$秒时,∠EPF=90°.