题目内容
9.已知一次函数y=2x+2与x轴y轴分别交于A、B两点,另一直线y=kx+3交x轴正半轴于E、交y轴于F点,如△AOB与E、F、O三点组成的三角形相似,那么k值为( )| A. | -0.5 | B. | -2 | C. | -0.5或-2 | D. | 以上都不对 |
分析 根据直线解析式求出点A、B、F的坐标,再根据相似三角形对应边成比例分OE和OA、OB是对应边两种情况讨论求出OE的长,然后求出直线y=kx+3的解析式,即可得解.
解答 解:∵一次函数y=2x+2与x轴y轴交于A、B两点,
∴A(-1,0),B(0,2),
∴OA=1,OB=2,
∵直线y=kx+3交y轴于F点,
∴F(0,3),
∴OF=3,
∵△AOB与E、F、O三点组成的三角形相似,
∴$\frac{OE}{OA}$=$\frac{OF}{OB}$或$\frac{OE}{OB}$=$\frac{OF}{OA}$,
即$\frac{OE}{1}$=$\frac{3}{2}$或$\frac{OE}{2}$=$\frac{3}{1}$,
解得OE=$\frac{3}{2}$或OE=6,
当OE=$\frac{3}{2}$时,y=-2x+3,
或OE=6时,y=-$\frac{1}{2}$x+3,
所以,k=-2或-$\frac{1}{2}$.
故选:C.
点评 本题考查了相似三角形对应边成比例的性质,两直线相交的问题,难点是要分情况讨论.

练习册系列答案
相关题目
20.若等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,则x的取值范围是( )
| A. | x≥2 | B. | x≥1 | C. | -1≤x≤2 | D. | x≤-1或x≥2 |
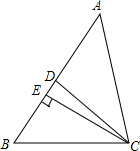 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.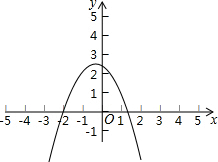 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a>b;③a-b+c>0;④4ac-8a>b2,其中正确的是①③(填序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a>b;③a-b+c>0;④4ac-8a>b2,其中正确的是①③(填序号) 如图,在⊙O中,AB为⊙O的弦,点C为圆上异于A、B的一点,∠OAB=25°,则∠ACB=65°.
如图,在⊙O中,AB为⊙O的弦,点C为圆上异于A、B的一点,∠OAB=25°,则∠ACB=65°.