题目内容
6.在△ABC中,BC=8,如图甲,B1是AB的中点,BC∥B1C1,则B1C1=4;
如图乙,B1、B2是AB的三等分点,BC∥B1C1∥B2C2,则B1C1+B2C2=8;
如图丙,B1、B2、…、Bn-1是AB的n等分点,BC∥B1C1∥B2C2∥…∥Bn-1Cn-1,则BC+B1C1+B2C2+…+Bn-1Cn-1=4(n+1).
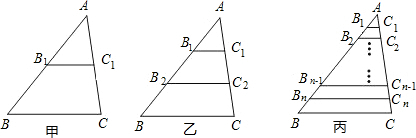
分析 根据相似三角形的性质,和等分点求出边与BC的相似比,找到规律,计算BC+B1C1+B2C2+…+Bn-1Cn-1的值.
解答 解:在图甲中∵BC∥B1C1,
∴$\frac{A{B}_{1}}{AB}$=$\frac{{B}_{1}{C}_{1}}{CB}$,
∵B1是AB的中点,
∴B1C1=$\frac{1}{2}$BC=4,
在图乙中,∵B1、B2是AB的三等分点,BC∥B1C1∥B2C2,
∴$\frac{{B}_{1}{C}_{1}}{BC}$=$\frac{A{B}_{1}}{AB}$=$\frac{1}{3}$,$\frac{{B}_{2}{C}_{2}}{BC}$=$\frac{A{B}_{2}}{BC}$=$\frac{2}{3}$,
∴B1C1=$\frac{1}{3}$BC,B2C2=$\frac{2}{3}$BC,
∴B1C1+B2C2=$\frac{1}{3}$BC+$\frac{2}{3}$BC=BC=8,
那么在图丙中,B1C1=$\frac{1}{n}$BC,B2C2=$\frac{2}{n}$BC,…Bn-1Cn-1=$\frac{n-1}{n}$BC,
∴BC+B1C1+B2C2+…+Bn-1Cn-1=4(n+1).
故答案为:4;8;4(n+1).
点评 本题主要利用相似三角形的性质和等分点求出边与BC的相似比,找出规律是关键.

练习册系列答案
相关题目
17.下列各数,不是无理数的是( )
| A. | 0.5 | |
| B. | $\sqrt{8}$ | |
| C. | 3π | |
| D. | 0.282282228…(两个8之间依次多1个2) |
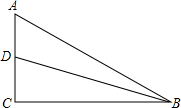 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,交AC于D,若CD=3,AB=8,则△ABD的面积12.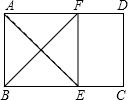 如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.
如图,在矩形ABCD中,∠A的平分线交BC于E,∠B的平分线交AD于F,求证:四边形ABEF是正方形.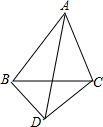 在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.
在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.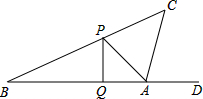 如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
如图:小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.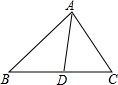 如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.
如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.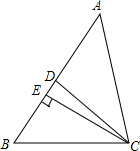 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.