题目内容
1. 如图,一次函数的图象经过点M,与x轴交于点A,与y轴交于点B,求S△AOB.
如图,一次函数的图象经过点M,与x轴交于点A,与y轴交于点B,求S△AOB.
分析 根据点B、M的坐标,利用待定系数法即可求出直线AB的解析式,由一次函数图象上点的坐标特征即可求出点A的坐标,再根据三角形的面积公式即可求出S△AOB的值.
解答 解:设一次函数的解析式为y=kx+b,
∵该一次函数的图象经过点M(-1,4)、B(0,6),
∴$\left\{\begin{array}{l}{-k+b=4}\\{b=6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴该一次函数的解析式为y=2x+6.
当y=2x+6=0时,x=-3,
∴点A的坐标为(-3,0),
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×3×6=9.
点评 此题主要考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及三角形的面积,根据点B、M的坐标,利用待定系数法即可求出直线AB的解析式是解题的关键.

练习册系列答案
相关题目
12. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )| A. | (144,0) | B. | (142,2) | C. | (72,0) | D. | (142,1) |
6.下列事件中,是必然事件的为( )
| A. | 明天会下雨 | B. | x是实数,x2<0 | ||
| C. | 两个奇数之和为偶数 | D. | 异号两数相加,和为负数 |
13.下列图形可由平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
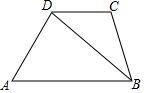 如图,已知四边形ABCD中,∠BCD=100°,BD平分∠ABC,且∠ABD=40°.
如图,已知四边形ABCD中,∠BCD=100°,BD平分∠ABC,且∠ABD=40°. 如图:
如图: 如图,四边形ABCD是某公园里的长方形风景区,长AB=50m,宽BC=25m,为方便有人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,若小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
如图,四边形ABCD是某公园里的长方形风景区,长AB=50m,宽BC=25m,为方便有人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,若小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )