题目内容
1.已知二次函数y1=ax2+bx+c(b≠c)图象的最高点坐标为(-2,4),则一次函数y2=(b-c)x+b2-4ac图象可能在( )| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
分析 根据题意得出y1=a(x+2)2+4,展开为y1=ax2+4ax+4a+4,即可得出b=4a,c=4a+4,从而得出b-c=-4,然后求得△=(4a)2-4a(4a+4)=-16a>0,即可判断一次函数y2=(b-c)x+b2-4ac图象所处的位置.
解答 解:由题意得y1=a(x+2)2+4,即y1=ax2+4ax+4a+4,
∴b=4a,c=4a+4,
∴b-c=-4,
∴△=(4a)2-4a(4a+4)=-16a,
∵a<0,
∴△=-16a>0.
故一次函数y2=(b-c)x+b2-4ac的图象可能在第一、二、四象限.
故选B.
点评 本题考查了二次函数的最值和一次函数的图象,对于二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点位置,抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
16.如图,在平面直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△AOB连续旋转变换,依次得到△1,△2,△3,△4…,则△2017的直角顶点的坐标为( )


| A. | (4032,0) | B. | (4036,0) | C. | (8064,0) | D. | (8068,0) |
6.已知二次函数y=x2-(m+1)x-5m(m为常数).在-1≤x≤3的范围内至少有一个x的值使y≥2,则m的取值范围是( )
| A. | m≤0 | B. | 0≤m≤$\frac{1}{2}$ | C. | m≤$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
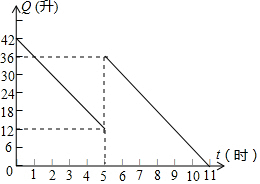 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.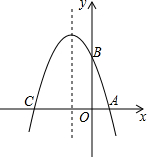 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.