题目内容
15.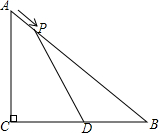 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
分析 根据勾股定理求出斜边AB,根据等腰三角形的判定得出符合情况的三种情况:①BP=PD,②BP=BD,③BD=PD,根据等腰三角形的性质得出即可.
解答  解:在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,
解:在Rt△ABC中,∠ACB=90°,AC=3cm,BC=4cm,
∴AB=5cm,
由运动可知,AP=t,且△DBP为等腰三角形有三种可能:
①若BP=PD,则∠B=∠PDB,
过P点作PE⊥BD于E,如图1,
∴BE=DE=$\frac{1}{2}$BD=$\frac{1}{4}$BC=1cm,
∵∠ACB=90°,
∴PE∥AC,
∴△PEB∽△ACB,
∴$\frac{BP}{AB}$=$\frac{EB}{BC}$,即$\frac{5-t}{5}$=$\frac{1}{4}$,
解得t=$\frac{15}{4}$;
②若BP=BD,则5-t=2,
解得t=3;
③若BD=PD,过点D作DH⊥AB,如图2,
则BH=$\frac{1}{2}$PB=$\frac{1}{2}$(5-t),
∵∠DHB=∠C=90°∠DBH=∠ABC,
∴△DBH∽△ABC,
∴$\frac{BH}{BC}$=$\frac{BD}{AB}$,即$\frac{\frac{1}{2}(5-t)}{4}$=$\frac{2}{5}$,
∴t=$\frac{9}{5}$;
综上所述,符合要求的t的值有3个,分别是$\frac{15}{4}$秒或3秒或$\frac{9}{5}$秒.
点评 本题考查了等腰三角形的性质和判定,勾股定理,能求出符合情况的所有情况是解此题的关键,用了分类讨论思想.

练习册系列答案
相关题目
6.计算(-x2y3)3•(-xy2)的结果是( )
| A. | -x7y11 | B. | x7y11 | C. | x6y8 | D. | -x7y8 |
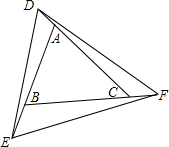 如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.
如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.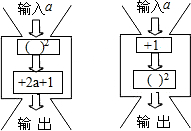 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?