题目内容
20.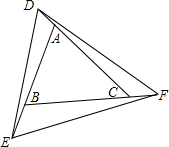 如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.
如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.
分析 根据三角形的外角的性质得到∠DEF=60°,根据三角形内角和定理求出∠EDF的度数,同理求出∠BAC的度数.
解答 解:∵∠ABC=∠BEF+∠BFE=60°,∠AED=∠BFE,
∴∠BEF+∠AED=60°,
∴∠DEF=60°,又∠DFE=50°,
∴∠EDF=180°-∠DEF-∠DFE=70°,
∵∠ACB=∠CFD+∠CDF=∠CFD+∠BFE=50°,
∴∠BAC=180°-60°-50°=70°.
点评 本题考查的是三角形内角和定理和三角形的外角的性质,掌握三角形内角和等于180°和三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.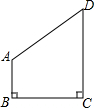 如图,∠C=∠B=90°,AB=5,BC=8,CD=11,则AD的长为( )
如图,∠C=∠B=90°,AB=5,BC=8,CD=11,则AD的长为( )
 如图,∠C=∠B=90°,AB=5,BC=8,CD=11,则AD的长为( )
如图,∠C=∠B=90°,AB=5,BC=8,CD=11,则AD的长为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
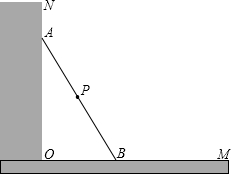 如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.
如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.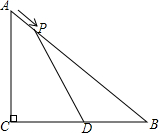 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值. 在△ABC中,AB=AC,AB=13,BC=10,BD⊥AC于D.
在△ABC中,AB=AC,AB=13,BC=10,BD⊥AC于D.