题目内容
18.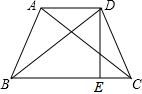 如图,在等腰梯形ABCD中,AD∥BC,DE⊥BC于E,若DE=3,BD=5,求梯形ABCD的面积.
如图,在等腰梯形ABCD中,AD∥BC,DE⊥BC于E,若DE=3,BD=5,求梯形ABCD的面积.
分析 过D作DF∥AC交BC的延长线与F,得到平行四边形ADFC和等腰直角三角形BDF,推出AD=CF,DE=BE=EF,求出BE和DF长度即可求出答案.
解答 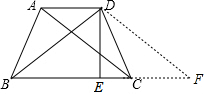 解:过D作DF∥AC交BC的延长线与F,
解:过D作DF∥AC交BC的延长线与F,
∵等腰梯形ABCD,AD∥BC,
∴AC=BD,
∵DF∥AC,AD∥BC
∴四边形ADFC是平行四边形,
∴AC=DF,
∴BD=DF=5,
∵DE⊥BC,
∴BE=EF=$\sqrt{B{D}^{2}-D{E}^{2}}$=4,
∴BF=8,
∴此梯形面积是:$\frac{1}{2}$×DE×BF=$\frac{1}{2}$×8×3=12,
答:此梯形的面积是12.
点评 本题主要考查对平行线的性质,等腰三角形的性质,直角三角形斜边上的中线性质,平行四边形的性质和判定,勾股定理,等腰梯形的性质等知识点的理解和掌握,能把梯形转化成平行四边形和等腰三角形是解此题的关键.

练习册系列答案
相关题目
3.已知点A(x1,y1),B(x2,y2)是反比例函数y=-$\frac{3}{x}$的图象上的两点,若x1<x2<0,则下列结论正确的是( )
| A. | y1<0<y2 | B. | y2<0<y1 | C. | 0<y1<y2 | D. | y1<y2<0 |
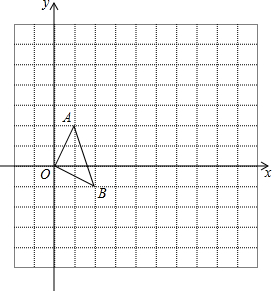 如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1). 如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM.
如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM.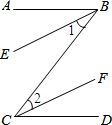 已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.