题目内容
9.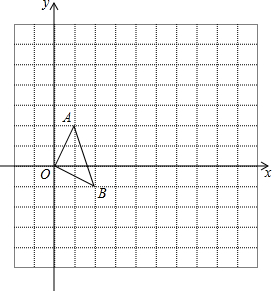 如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).(1)以点O(0,0)为位似中心,按比例尺(OA:OA′)1:2在位似中心的同侧将△OAB放大为△OA′B′,放大后点A、B的对应点分别为A′、B′.画出△OA′B′,并写出点A′、B′的坐标:A′(2,4 ),B′(4,-2);
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C'的坐标((2a,2b)).
分析 (1)利用位似图形的性质得出对应点位置进而求出即可;
(2)利用位似图形的性质结合位似比进而求出即可.
解答  解:(1)如图所示:△OA′B′即为所求,
解:(1)如图所示:△OA′B′即为所求,
点A′的坐标:A′(2,4),点B′的坐标:B′(4,-2);
(2)在(1)中,C(a,b)为线段AB上任一点,点C的对应点C'的坐标为:(2a,2b).
故答案为:(2a,2b).
点评 此题主要考查了位似变换,根据题意得出对应点位置是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
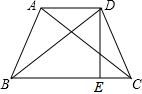 如图,在等腰梯形ABCD中,AD∥BC,DE⊥BC于E,若DE=3,BD=5,求梯形ABCD的面积.
如图,在等腰梯形ABCD中,AD∥BC,DE⊥BC于E,若DE=3,BD=5,求梯形ABCD的面积.